Reconstruction-free cascaded ACS method
We introduce a novel reconstruction-free cascaded Adaptive Compressive Sensing
(ACS) framework, which obviates the need for reconstruction at the adaptive sampling process.
A lightweight ScoreNet is proposed to allocate sampling rates based on the previous CS measurements
and a differentiable adaptive sampling module is designed for end-to-end training.
Furthermore, we propose a Multi-Grid Spatial-Attention Network (MGSANet) for efficient multi-stage training and reconstruction.
By incorporating reconstruction fidelity supervision outside the adaptive sampling loop,
we optimize ACS for high-quality imaging.
Reconstruction-free cascaded ACS framework
As shown in Figure 1, we propose a multi-stage framework for realizing reconstruction-free ACS.
The overall ACS framework is composed of three main parts, including the multi-stage ACS backbone,
the forward adaptive sampling method, and the final image reconstruction with the input of all the ACS measurements.
Furthermore, the forward adaptive sampling method is composed of ScoreNet and an adaptive sampling module,
which first scores the previous measurements of each block and then implements the adaptive sampling based on the score.
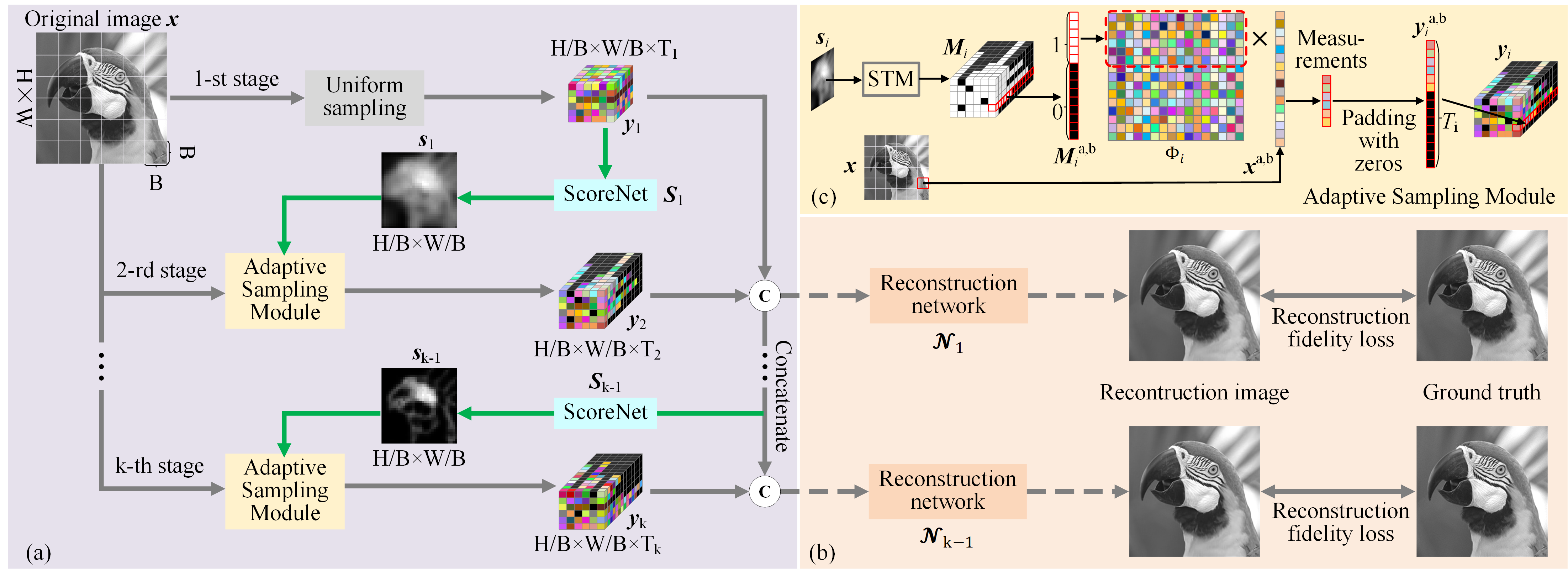
Figure 2. The overview of the proposed reconstruction-free adaptive CS method,
the multi-stage adaptive sampling can be conducted without reconstruction until the target CS sampling rate is achieved.
(a) The multi-stage ACS sampling process, (b) the reconstruction process and the out-of-loop
reconstruction-fidelity supervision during the training process, and (c) the structure of the ASM.
LP-based differentiable adaptive sampling
To realize adaptive sampling based on previous measurements, we propose two modules,
i.e., the lightweight ScoreNet module and the adaptive sampling module, which score each block with previous measurements
and implement adaptive sampling based on the score.
For the adaptive sampling module, we propose to decide the number of required measurement of the block and
select the first corresponding number of rows of the whole measurement matrix $\Phi_i \in \mathbb{R}^{T_i\times B^2}$ to
form the real measurement matrix of the block at stage $i$, as shown in Figure 2(c).
$T_i$ is a hyper-parameter constraining block measurement counts, ensuring the sampling rate does not exceed 1.
Specifically, we introduce a Score To Mask (STM) module to generate a binary selection mask $\boldsymbol{M}_i$ based on
${\boldsymbol s}_i$. The measurement of each image block is thus $\boldsymbol{y}_i^{a,b} =
\boldsymbol{M}_i^{a,b} \odot (\Phi_i\boldsymbol{x}^{a,b})$, where $\odot$ denotes the dot product.
Through introducing an auxiliary variable
\begin{equation}
\boldsymbol{\eta}_i = C\left[\boldsymbol{s}_i; \boldsymbol{s}_i-1/{m_i}; ...;\boldsymbol{s}_i-{(T_i-1)}/{m_i}\right ], \tag{1}
\label{equation1}
\end{equation}
where $C[\cdot]$ is the concatenate operation in the third dimension and
$\boldsymbol{\eta}_i \in \mathbb{R}^{\frac{H}{B}\times \frac{W}{B} \times T_i}$.
$m_i$ is the total number of measurements at stage $i$. For a given sampling rate $r_i$ of $i$-th sampling stage
and an image with $H\times W$ pixels, $m_i=H\times W\times r_i$. We propose the STM module as
\begin{equation}
\boldsymbol{M}_i = \mathrm{Binarize}(\boldsymbol{\eta}_i - \tau_i), \tag{2}
\label{equation2}
\end{equation}
where $\tau_i$ is the $m_i$-th largest value in $\boldsymbol{\eta}_i$.
However, Equation \eqref{equation2} is non-differentiable. To address this issue,
we propose to construct an integer linear programming problem,
which can be differentiated with the perturbed optimizer. The constructed LP problem is
\begin{equation}
\begin{aligned}
\mathop{\mathrm{arg\; max}}\limits_{\boldsymbol{M}_i\in \mathcal{C}}\langle\boldsymbol{M}_i, &\boldsymbol{\eta}_i\rangle, \\
s.t.\;\mathcal{C}=\{ \boldsymbol{M}_i \in \{0,1\}^{\frac{H}{B}\times \frac{W}{B}\times T_i}: & \sum_{a,b,t} \boldsymbol{M}_i^{a,b,t} = m_i, \\
M_i^{a,b,t} \geq M_i^{a,b,t+1}, &\forall t\in \{1,...,T_i-1\} \},
\label{eq: STM_in_LP_form}
\end{aligned}
\tag{3}
\end{equation}
where $t$ indexes the third dimension of $\boldsymbol{M}_i$. $\mathcal{C}$ is the convex polytope set that meets two conditions.
The first condition constrains the total number of selected measurements to be $m_i$, and the second condition denotes
that we select the first several rows of the sampling matrix $\Phi_i$. In the training process,
the forward and backward propagation of the LP-based differentiable STM are defined below.
\paragraph{Forward propagation:}
\begin{equation}
\begin{aligned}
\overline{\boldsymbol{M}_i} &= \mathbb{E}_Z \left [ \mathop{\mathrm{arg\; max}}\limits_{\boldsymbol{M}_i\in \mathcal{C}}\langle\boldsymbol{M}_i, \boldsymbol{\eta}_i+ \sigma \boldsymbol{Z}\rangle \right ], \\
& = \sum \limits_{q=1}^{Q}\left [ {\rm STM}(\boldsymbol{\eta}_i+ \sigma \boldsymbol{Z}_q)\right ], \\
\end{aligned}
\tag{4}
\end{equation}
where $Q$ different uniform Gaussian noise $\boldsymbol{Z}_q$ is added to perturb the input $\boldsymbol{\eta}_i$ and the output is the expectation of the output of the LP module. $\sigma$ and $Q$ are hyper-parameters.
Backward propagation:
The backpropagation can be achieved with the Jacobian matrix and the Jacobian of the above forward propagation can be calculated as
\begin{equation}
\begin{aligned}
J_{\boldsymbol{s}}\boldsymbol{M}_i &= \mathbb{E}_Z \left [ \mathop{\mathrm{arg\; max}}\limits_{\boldsymbol{M}_i\in \mathcal{C}}\langle\boldsymbol{M}_i, \boldsymbol{\eta}_i + \sigma \boldsymbol{Z}\rangle \boldsymbol{Z}^T /\sigma \right ],\\
&= \sum \limits_{q=1}^{Q} \left [ {\rm STM} \left (\boldsymbol{\eta}_i + \sigma \boldsymbol{Z}_q \right ) \boldsymbol{Z}_q^T /\sigma\right ].\\
\end{aligned}
\tag{5}
\end{equation}
MGSANet-based reconstruction network
For efficient training and inferencing, we propose a multi-grid spatial attention network,
as shown in Figure 3. Due to GPUs' parallel computing strength,
networks with greater parallelism achieve faster acceleration than less parallel models at the same FLOPs.
Consequently, we propose the integration of a multi-grid structure as the fundamental backbone of our architecture.
This structure facilitates the distribution of features across multiple branches, enabling parallel processing.
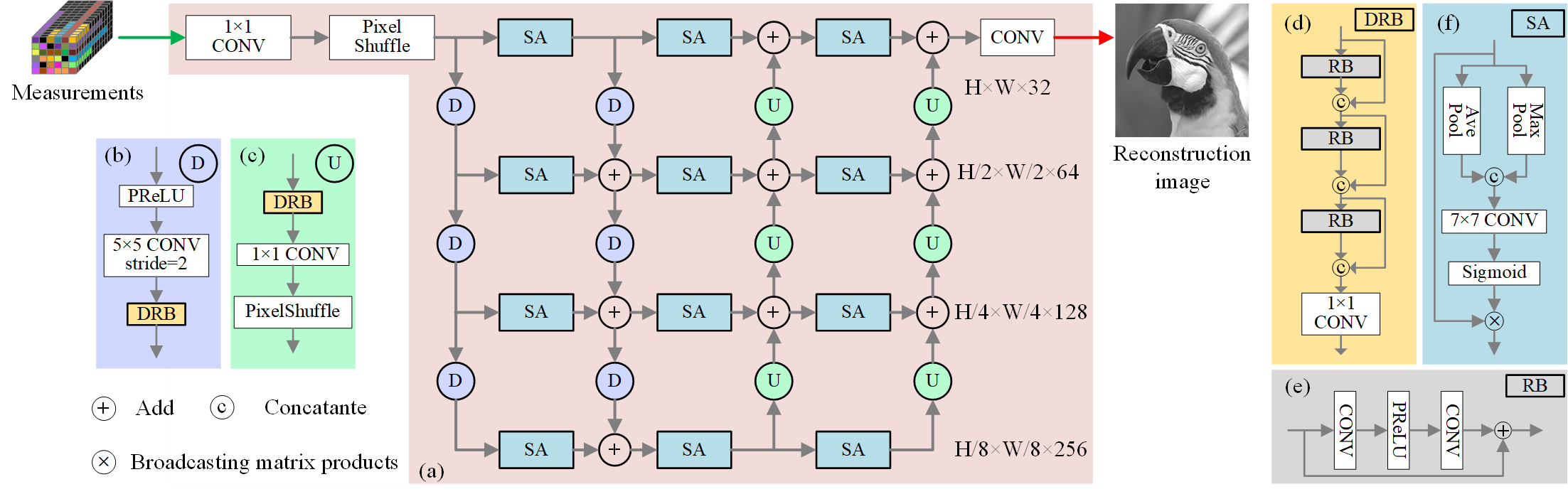
Figure 3. The overall structure of the proposed MGSANet. (a) The backbone of MGSANet,
(b) upsampling module, (c) downsampling module, (d) Dense Residual Block, (e) Residual Block, and (f) Spatial Attention module.
|
Experiments
Quantitative results
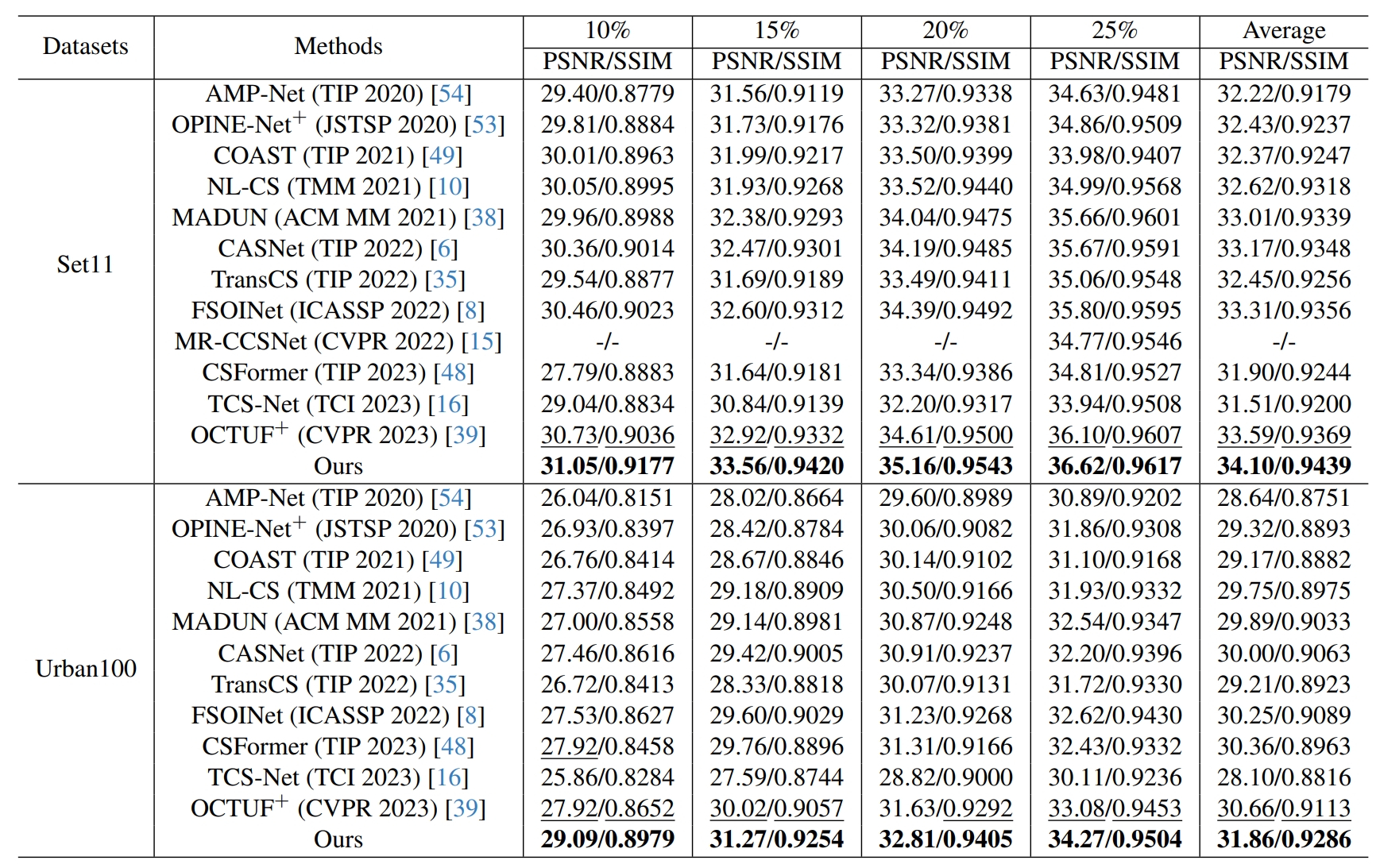
We compare our proposed model with state-of-the-art (SOTA) CS methods proposed in recently years,
which includes AMP-Net, OPINE-Net$^+$, COAST, NL-CS, MADUN, CASNet, TransCS, FSOINet, CSFormer, TCS-Net and OCTUF$^+$.
The quantitative comparison is summarized in Table 1, we can observe that our proposed model can outperform the SOTA CS methods at the sampling rates of 10%, 15%, 20% and 25%.
Table 3. Performance comparison with state-of-the-art CS algorithms on Set11 and Urban100 test sets.
The bold font is utilized to indicate the best results and the second-best results are marked with an underline.
Visual results
Figure 4 shows the visual reconstruction results,
we can observe that the reconstruction results of our proposed method are closer to the ground truth and have clearer texture details.
In all, through comparison with the SOTA methods, we demonstrate the superiority of our proposed method both quantitatively and qualitatively.

Figure 4. Visual comparison with the state-of-the-art CS algorithms. Top row: Barbara from Set11
with sampling rate = 10%, bottom row: img_062 from Urban100 with sampling rate = 25%.
|




